Introduction
In the previous post we saw how to solve all-pairs shortest path problem using Floyd-Warshall algorithm. We also explored several ways to improve algorithm’s performance by using parallelism and vectorisation.
However, if you think about the results of the Floyd-Warshall algorithm, you will quickly realise the interesting moment – we know the distances (values of shortest paths) between vertexes in a graph but we don’t know the “routes” i.e. we don’t know what vertexes contribute to each shortest path, and we can’t rebuild these “routes” from the results we have.
In this post, I invite you to join me and extend the Floyd-Warshall algorithm. This time, we are going to make sure we can calculate the distance and rebuild the “route”.
A bit of known theory…
Before diving into code and benchmarks, let’s revise a theory of how Floyd-Warshall algorithm works.
Here is a textual description of the algorithm:
- We start from representing a graph (
G) of sizeNas matrix (W) of sizeN x Nwhere every cellW[i,j]contains a weight of an edge from vertexito vertexj(see Picture 1). In cases when there is no edge between vertexes the cell is set to a specialNO_EDGEvalue (shown as dark cells on Picture 1). - From now on, we say –
W[i,j]contains a distance between vertexesiandj. - Next, we take a vertex
kand iterate through all pairs of vertexesW[i,j]checking if distancei ⭢ k ⭢ jis smaller than currently known distance betweeniandj. - The smallest value is stored in
W[i,j]and step #3 is repeated for the nextkuntil all vertexes ofGhave been used ask.

Here is the pseudo-code:
algorithm FloydWarshall(W) do
for k = 0 to N - 1 do
for i = 0 to N - 1 do
for j = 0 to N - 1 do
W[i,j] = min(W[i,j], W[i,k] + W[k,j])
end for
end for
end for
end algorithm
When done, every cell W[i,j] of matrix W either contains a distance of shortest path between vertexes i and j or a NO_EDGE value, if there is no path between them.
As I mentioned in the beginning – having only this information makes it impossible to reconstruct the routes between these vertexes. So… what should we do to be able to reconstruct these routes?
Well… it may sound obvious but… we need to collect more data!
… a bit of same theory but from a different angle
The essence of the Floyd-Warshall algorithm is a compartment of known distance W[i,j] with a distance of potentially new path from i to j through intermediate vertex k.
I drag so much attention to this detail because it is the key to how we can preserve routes information. Let’s take the previous graph of 5 vertexes (see Picture 2) and execute the Floyd-Warshall algorithm on it.
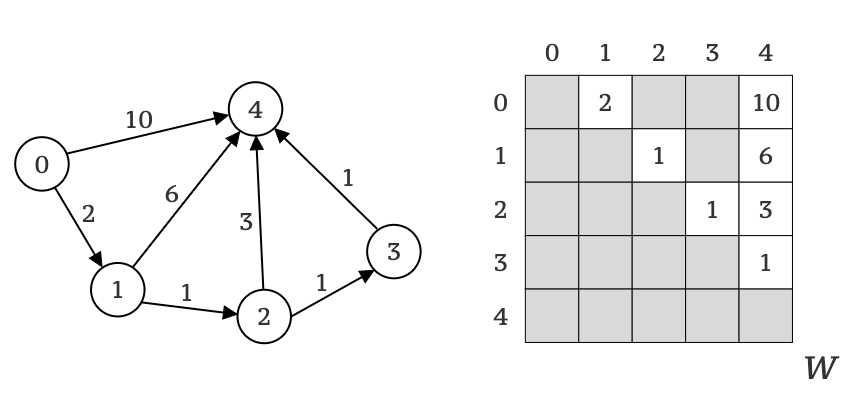
Initially, we know about all graph edges, which gives us the following paths: 0 ⭢ 1 :2, 0 ⭢ 4 :10, 1 ⭢ 3 :1, 2 ⭢ 4 :1, 3 ⭢ 2 :1 and 3 ⭢ 4 :3.
I use the “from” ⭢ “to” :”distance” format from the previous post to write down paths.
Author’s note
We also know, there are no edges lead to vertex 0, so executing an algorithm for k = 0 makes no sense. It is also obvious, there is a single edge (0 ⭢ 1) leading to from vertex 0 to vertex 1, which also makes execution of all i != 0 (the i is “from” here) quite meaningless and because vertex 1 has edges with 2 and 4, it also makes no sense to execute algorithms for any j which isn’t 2 or 4 (the j is “to” here).
That is why our first step will be to execute an algorithm for k = 1, i = 0 and j = 2,4.
| Step | Path | Comment |
|---|---|---|
| 1 | 0 ⭢ 1 ⭢ 2 | Path found. Distance = 3 (was nothing) |
| 2 | 0 ⭢ 1 ⭢ 4 | Path found. Distance = 8 (was 10). |
We have found two paths: a new path (0 ⭢ 1 ⭢ 2) and a shortcut (0 ⭢ 1 ⭢ 4). Both go through vertex 1. If we don’t store this information (the fact we got to 2 and 4 through 1) somewhere right now it will be lost forever (and that is quite the opposite of what we want).
So what should we do? We will update matrix W with new values (see Picture 3a) and also store the value of k (which is k = 1) in cells R[0,2] and R[0,4] of a new matrix R of same size as matrix W but initialised with NO_EDGE values (see Picture 3b).

Right now, don’t focus on what exactly matrix R is. Let’s just keep going and execute algorithm for the next k = 2.
Here are will do the same analysis (to understand what combinations make sense to execute) as we did for k = 1 but this time we will use matrix W instead of graph G. Look at the matrix W, especially at column #2 and row #2 (Picture 4).
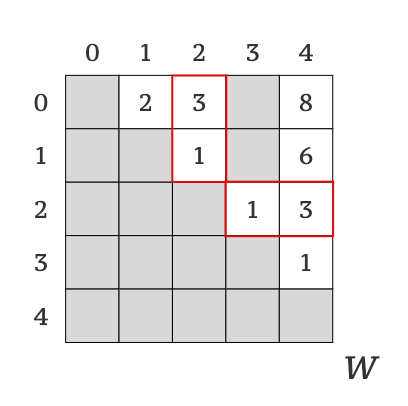
Here you can see, there are two paths to vertex 2, from vertex 0 and from vertex 1 (column #2), and two paths from vertex 2, to vertex 3 and to vertex 4 (row #2). Knowing that, it makes sense to execute algorithm only for combinations of k = 2, i = 0,1 and j = 3,4.
| Step | Path | Comment |
|---|---|---|
| 1 | 0 ⭢ 2 ⭢ 3 | Path found. Distance = 4 (was nothing) |
| 2 | 0 ⭢ 2 ⭢ 4 | Path found. Distance = 6 (was 8) |
| 3 | 1 ⭢ 2 ⭢ 3 | Path found. Distance = 2 (was nothing) |
| 4 | 1 ⭢ 2 ⭢ 4 | Path found. Distance = 4 (was 6) |
As we have already done previously, we are updating cells W[0,3], W[0,4], W[1,3], W[1,4] with new distances and cells R[0,3], R[0,4], R[1,3] and R[1,4] with k = 2 (see Picture 5).

There is only k = 3 is left to process (because there are no edges leading from vertex 4 to any other vertex in the graph).
Again, let’s take a look at the matrix W (Picture 6).

According to the matrix W there are three paths to vertex 3, from vertexes 0, 1 and 2 (column #3), and there is one path from vertex 3 to vertex 4 (row #3). Therefore we have the following paths to process:
| Step | Path | Comment |
|---|---|---|
| 1 | 0 ⭢ 3 ⭢ 4 | Path found. Distance = 5 (was 6) |
| 2 | 1 ⭢ 3 ⭢ 4 | Path found. Distance = 3 (was 4) |
| 3 | 2 ⭢ 3 ⭢ 4 | Path found. Distance = 2 (was 3) |
This was the last iteration of the algorithm. All what is left, is to update cells W[0,4], W[1,4], W[2,4] with new distances and set cells R[0,4], R[1,4], R[2,4] to 3.
Here is what we have at the end of the algorithm (Picture 7).

As we know from the previous post, matrix W now contains all-pairs of shortest paths in graph G. But what is stored inside matrix R?
Homecoming
Every time we were finding a new shortest path we were updating the corresponding cell of matrix R with the current value of k. While at first, this action might look mysterious it has a very simple meaning – we were storing the vertex, from which we reached the destination vertex: i ⭢ k ⭢ j (here we are reaching j directly from k)
This moment is crucial. Because knowing a vertex we came from allows us to rebuild the route by moving backwards (like a lobster) from the vertex j (the “to”) to vertex i (the “from”).
Here is a textual description of the algorithm to rebuild the route from i to j:
- Prepare empty dynamic array
X. - Start from reading a value
zfrom cellR[i,j]. - If
zisNO_EDGE, then the route fromitojis found and we should proceed to step #7. - Prepend
zto a dynamic arrayX. - Read value of cell
R[i,z]intoz. - Repeat steps #3, #4 and #5 until exit condition in #3 is reached.
- Prepend
ito X. - Append
jtoX. - Now dynamic array
Xcontains the route fromitoj.
Please note, the above algorithm works only for existing paths. It also isn’t perfect from performance point of view and for sure can be optimised. However, in scope of this post it is specifically described in such a way to make it easier to understand and reproduce on a sheet of paper.
Author’s note
In pseudo-code it looks even simpler:
algorithm RebuildRoute(i, j, R)
x = array()
z = R[i,j]
while (z ne NO_EDGE) do
x.prepend(z)
z = R[i,z]
end while
x.prepend(i)
x.append(j)
return x
end algorithm
Let’s try it on our graph G and rebuild a route from vertex 0 to vertex 4 (see Picture 8).
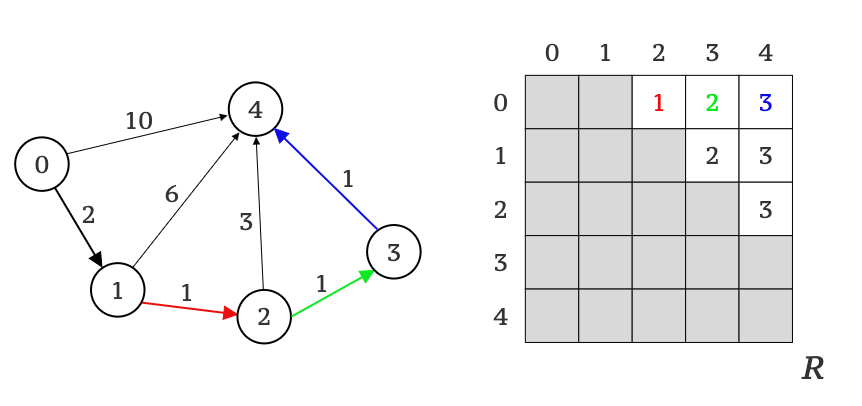
Here is a textual description of the above illustration:
- We start from reading the value from
R[0,4], which results in3. According to the algorithm this means the route goes to vertex4from vertex3(shown in BLUE). - Because the value of
R[0,4]isn’tNO_EDGEwe proceed and read value ofR[0,3]which results in2(shown in GREEN). - Again, because value of
R[0,3]isn’tNO_EDGE, we proceed and read value ofR[0,2]which results in1(shown in RED). - At last, we read a value of
R[0,1], which results in theNO_EDGEvalue, meaning, there are no more vertexes except0and4which contribute to the route. Therefore, the resulting route is:0 ⭢ 1 ⭢ 2 ⭢ 3 ⭢ 4which if you look at the graph is indeed corresponds to the shortest path from vertex0to vertex4.
A thoughtful reader might ask:
How can we be sure that all data we read from matrix
Thoughtful readerRbelongs to the same path?
It is a very good question. We are sure because we update matrix R with new value when we update the shortest path value in matrix W. So in the end, every row of matrix R contains data related to shortest paths. No more, no less.
Now, we are done with the theory, it is an implementation time.
Implementation in C#
In the previous post besides implementing an original version of Floyd-Warshall algorithm, we have also integrated various optimisations: support for sparse-graphs, parallelism, vectorisation and in the end we also combined them all.
There is no reason to repeat all of this today. However, I would like to show you how to integrate route memorisation into original and vectorised (with support for sparse-graphs) versions of the algorithm.
Integration into original algorithm
It might be hard to believe but to integrate route memorisation into original version of the algorithms all we need to do is to:
- Extend function signature to include
Rmatrix as separate parameter –int[] routes. - Save k to
routesevery time shortest path is changed (line: 14).
That is it. Just one and a half lines of code:
public void FloydWarshallRoutes_00(
int[] matrix, int[] routes, int sz)
{
for (var k = 0; k < sz; ++k)
{
for (var i = 0; i < sz; ++i)
{
for (var j = 0; j < sz; ++j)
{
var distance = matrix[i * sz + k] + matrix[k * sz + j];
if (matrix[i * sz + j] > distance)
{
matrix[i * sz + j] = distance;
routes[i * sz + j] = k;
}
}
}
}
}
Integration into vectorised algorithm
Integration into vectorised (with support for sparse-graphs) version takes a bit more effort to complete, however the conceptual steps are the same:
- Extend function signature to include
Rmatrix as separate parameter –int[] routes. - On each iteration, initialise a new vector of
kvalues (line: 6). - Save
kvalues vector toroutesevery time shortest path is changed (lines: 31-32). - Update a non-vectorised part of the algorithm in the same way as we updated the original algorithm (line: 41).
public void FloydWarshallRoutes_01(
int[] matrix, int[] routes, int sz)
{
for (var k = 0; k < sz; ++k)
{
var k_vec = new Vector<int>(k);
for (var i = 0; i < sz; ++i)
{
if (matrix[i * sz + k] == Constants.NO_EDGE)
{
continue;
}
var ik_vec = new Vector<int>(matrix[i * sz + k]);
var j = 0;
for (; j < sz - Vector<int>.Count; j += Vector<int>.Count)
{
var ij_vec = new Vector<int>(matrix, i * sz + j);
var ikj_vec = new Vector<int>(matrix, k * sz + j) + ik_vec;
var lt_vec = Vector.LessThan(ij_vec, ikj_vec);
if (lt_vec == new Vector<int>(-1))
{
continue;
}
var r_vec = Vector.ConditionalSelect(lt_vec, ij_vec, ikj_vec);
r_vec.CopyTo(matrix, i * sz + j);
var ro_vec = new Vector<int>(routes, i * sz + j);
var rk_vec = Vector.ConditionalSelect(lt_vec, ro_vec, k_vec);
rk_vec.CopyTo(routes, i * sz + j);
}
for (; j < sz; ++j)
{
var distance = matrix[i * sz + k] + matrix[k * sz + j];
if (matrix[i * sz + j] > distance)
{
matrix[i * sz + j] = distance;
routes[i * sz + j] = k;
}
}
}
}
}
A small reminder –
Author’s noteVector.ConditionalSelectoperation returns a new vector where values are equal to smaller of two corresponding values of input vectors i.e., if value of vectorlt_vecis equal to-1, then operation selects a value fromij_vec, otherwise it selects a value fromk_vec.
Benchmarking
Collecting routes information seems reasonable enough because… well why not? Especially when it is so easy to integrate into existing algorithms. However, let’s see how practical it is to integrate it by default.
Here are two set of benchmarks: with and without (both execute original and vectorised versions of the algorithm). All benchmark were executed by BenchmarkDotNet v0.13.1 (.NET 6.0.4 x64) on a machine equipped with an Intel Core i5-6200U CPU 2.30GHz (Skylake) processor and running Windows 10 .
All experiments were executed on the predefined set of graphs used in the previous post: 300, 600, 1200, 2400 and 4800 vertexes.
You can find experimental graphs as well as source code on GitHub.
Author’s note
Below are the benchmark results where *_00 and *Routes_00 methods correspond to original version of the algorithm and *_03 and *Routes_01 methods correspond to vectorised (with support for sparse-graphs) version of the algorithm.
| Method | Size | Mean (ms) | Error (ms) | StdDev (ms) |
|---|---|---|---|---|
| FloydWarshall_00 | 300 | 40.233 | 0.0572 | 0.0477 |
| FloydWarshallRoutes_00 | 300 | 40.349 | 0.1284 | 0.1201 |
| FloydWarshall_03 | 300 | 4.472 | 0.0168 | 0.0140 |
| FloydWarshallRoutes_01 | 300 | 4.517 | 0.0218 | 0.0193 |
| FloydWarshall_00 | 600 | 324.637 | 5.6161 | 4.6897 |
| FloydWarshallRoutes_00 | 600 | 321.173 | 1.4339 | 1.2711 |
| FloydWarshall_03 | 600 | 32.133 | 0.2151 | 0.1679 |
| FloydWarshallRoutes_01 | 600 | 34.646 | 0.1286 | 0.1073 |
| FloydWarshall_00 | 1200 | 2,656.024 | 6.9640 | 5.8153 |
| FloydWarshallRoutes_00 | 1200 | 2,657.883 | 8.8814 | 7.4164 |
| FloydWarshall_03 | 1200 | 361.435 | 2.5877 | 2.2940 |
| FloydWarshallRoutes_01 | 1200 | 381.625 | 3.6975 | 3.2777 |
| FloydWarshall_00 | 2400 | 21,059.519 | 38.2291 | 33.8891 |
| FloydWarshallRoutes_00 | 2400 | 20,954.852 | 56.4719 | 50.0609 |
| FloydWarshall_03 | 2400 | 3,029.488 | 12.1528 | 11.3677 |
| FloydWarshallRoutes_01 | 2400 | 3,079.006 | 8.6125 | 7.1918 |
| FloydWarshall_00 | 4800 | 164,869.803 | 547.6675 | 427.5828 |
| FloydWarshallRoutes_00 | 4800 | 184,305.980 | 210.9535 | 164.6986 |
| FloydWarshall_03 | 4800 | 21,882.379 | 200.2820 | 177.5448 |
| FloydWarshallRoutes_01 | 4800 | 21,004.612 | 79.8752 | 70.8073 |
Benchmark results aren’t simple to interpret. If you take a closer look you will find combination when routes collection actually made algorithm to run faster or without any significant effect at all.
This looks very confusing (and if it is – I strongly advice you to listen this show with Denis Bakhvalov and Andrey Akinshin to better understand what tricky things can affect measurements). My best take here is that “confusing” behaviour is caused by great CPU cache performance (because graphs aren’t large enough to saturate caches). Partially this theory is based on the “bold” sample where we can see significant degradation on the largest graph. However, I didn’t verify it.
In general, the benchmark shows that if we aren’t talking about extremely high-performance scenarios and huge graphs, it is okay to integrate routes memorisation into both algorithms by default (but keep in mind it will double memory consumption because we need to allocate two matrices W and R instead of one).
The only thing left is an implementation of route rebuild algorithm.
Implementation of route rebuild algorithm
Implementation of route rebuild algorithms in C# is straightforward and almost completely reflects the previously demonstrated pseudo-code (we use LinkedList<T> to represent dynamic array):
public static IEnumerable<int> RebuildRoute_00(
int[] routes, int sz, int i, int j)
{
var x = new LinkedList<int>();
var z = routes[i * sz + j];
while (z != Constants.NO_EDGE)
{
x.AddFirst(z);
z = routes[i * sz + z];
}
x.AddFirst(i);
x.AddLast(j);
return x;
}
The above algorithm isn’t perfect and definitely can be improved. The simplest improvement we can make is to preallocate an array of sz size and fill it in reverse order:
public static IEnumerable<int> RebuildRoute_01(
int[] routes, int sz, int i, int j)
{
var x = new int[sz];
var y = sz - 1;
// Fill array from the end
x[y--] = j;
var z = routes[i * sz + j];
while (z != Constants.NO_EDGE)
{
x[y--] = z;
z = routes[i * sz + z];
}
x[y] = i;
// Create an array segment from 'y' to the end of the array
return new ArraySegment<int>(x, y, sz - y);
}
While this “optimisation” reduces the number of allocations to one, it doesn’t necessary makes the algorithm “faster” or “allocates less memory” than previous one. The point here is, if we need to have a route ordered from i to j we always will have to “reverse” the data we retrieve from matrix R and there is no way to escape it.
But if we can present data in reverse order then we can make use of LINQ and avoid any unnecessary allocations:
public static IEnumerable<int> RebuildRoute_Reverse_00(
int[] routes, int sz, int i, int j)
{
yield return j;
var z = routes[i * sz + j];
while (z != Constants.NO_EDGE)
{
yield return z;
z = routes[i * sz + z];
}
yield return i;
}
There can be many more variants of how this code can be “changed” or “improved”. The important moment here is to remember – any “change” has downsides in terms of memory or CPU cycles.
Feel free to experiment! The possibilities are almost limitless!
Conclusion
In this post we had a deep dive into the theory behind Floyd-Warshall algorithm and have extended it with a possibility to memorise shortest paths “routes”. Then we have updated C# implementations (original and vectorised) from the previous post. In the end we have implemented a few versions of the algorithm to rebuild the “routes”.
We have repeated a lot from previous post but at the same time I hope you have found something new and interesting in this one. This isn’t the end of the all-pairs shortest paths problem. This is just a beginning.
I hope you have enjoyed the reading and see you next time!
History
- 2023/04/08 – Updated source code of vectorised algorithm.
Replaced line #31 with two lines (now #31 and #32):
— previousvar rk_vec = Vector.ConditionalSelect(lt_vec, ij_vec, k_vec)
— currentvar ro_vec = new Vector<int>(routes, i * sz + j);
var rk_vec = Vector.ConditionalSelect(lt_vec, ro_vec, k_vec);
—
to address the issue when some of the routes are overwritten by the values from distance vector instead of being just updated with values fromk_vec.
Replaced line #42 (previously was #41):
— previousroutes[i * sz + j] = distance
— currentroutes[i * sz + j] = k
—
to writekvalue instead of distance into the route matrix.